中学受験をするには旅人算の習得は欠かせません。二人の人物が出会ったり、追いついたりするまでの時間や距離などを求める問題の練習から始め、おおよそ2年かけて複雑な設定の入試問題レベルまで学習していきます。
「算数で一番苦手な単元は?」と子どもたちに聞いて返ってくる回答に「旅人算」が挙がることはあまりありません。塾のプリントに出てくる典型題は、子どもたちにとっては比較的理解しやすいものが多いからかもしれません。しかし、きちんとしたプロセスを経て学習していかないと典型題しか解けず、その先のレベルに進めない可能性があります。ポイントをおさえて学習し、確実に得意単元にしていきましょう。
旅人算に必要な5つのスキル
旅人算を得意単元にするためには、どのような力が必要なのでしょうか。
①速さに対する理解
入試問題に出てくる速さは、日常生活の人や物の速さを基本としています。例えば自動車であれば、時速60㎞くらいでしょうか。人が歩いているなら分速70mあたり。このように自分や自分の周りにあるものの「だいたいの速さの感覚」がとても大切です。この感覚のある生徒さんは、自分の答えが「車の時速480㎞」と出たときに「何かおかしいな?」と思い、もう一度やり直してみることができます。
こうした感覚を身につけるために、例えばご旅行の際に「いま、高速道路を時速80㎞で走ってるね。あと120㎞で大きなサービスエリアがあるけど、どのくらいかかるかな?」といったような会話をしてみるのも効果的です。積極的に「速さ」を日常会話で使ってみせてあげましょう。
②単位の扱い
5年生で速さの単元に入ったとき、子どもたちが一番苦労するのが単位です。「分速60mで2分進んだ距離は?」にはすぐに答えられても、「時速3.6㎞で7分15秒進んだ距離は?」となると正答率は一気に下がります。これは単位の変換のテクニックがないことと、変換すること自体に慣れていないことが原因です。自己流ではなく塾の授業で習うやり方、解説にあるテクニックを真似ることから始めて反復練習していきましょう。「正しいテクニック」と「慣れ」の両方が必要です。
進度の速い塾の授業では、こうした技術習得にはわずかな時間しか割けないのが普通です。ご家庭での反復練習が必須となりますので、お子さんがスラスラと解けるようになるまで反復練習しましょう。
③線分図による和と差への注目
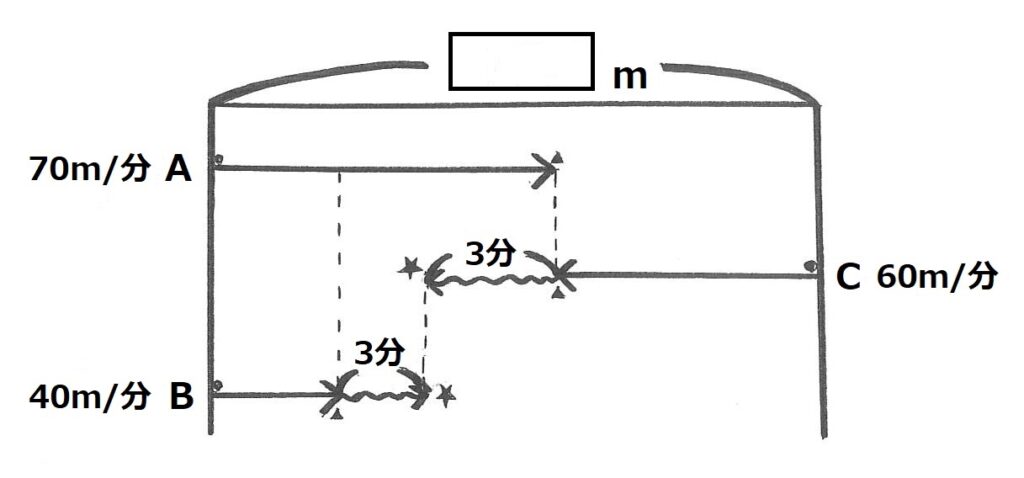
線分図
旅人算では人が動いた様子を線で表し、その和と差から解き口を見つけていきます。5年生後半になると、その図に比を書き込んで解いていきます。そのため、旅人算の授業では、講師は必ず黒板に図を描いて説明します。子どもたちは授業で説明された図を真似して練習することで、さらに条件の複雑な問題に対応する力をつけていくことができるのです。
ところが、解き方を理解したあと、図を省略しはじめる子どもたちがいます。図を描くように伝えても、「面倒だから」「時間がかかるから」「書かなくてもできるから」と書くことを避ける傾向があるのです。習いはじめの旅人算の典型題の場合、一度理解してしまえば図を描かなくても解けてしまうものが多いことも原因かもしれません。
しかし、典型題から入試レベルの問題にステップアップしていくためにも、しっかりと図を描きながら練習することを習慣にしましょう。真っ直ぐな線を描く、あるいは簡略化して短時間でポイントをおさえた図を描くには「場数を踏む」ことが大切です。普段から描いていなければ、いざ入試問題に取り組もうというときに制限時間内で図を描くことはできません。ご家庭でも、復習テストの点が良かったからと安心せずに「図を描きながら解いているか?」とチェックをしてみることをおすすめします。
④比の使用
5年前期では「図を描いて和と差から解く」解法で解いていた問題を、5年生の後半では「比」を使って解いていきます。「比」を使うほうが楽に計算できて、早く答えにたどりつけます。
ただし、抽象的な理解が必要になってくるので注意が必要です。よく使われる「同じ時間で進んだ距離の比は速さの比に等しい」「同じ距離を進む場合、時間の比と速さの比が逆比」などといった内容が、ただの暗記にとどまらずにきちんと理解されているかを確認したいところです。時間のあるときに、塾で習ってきた問題を説明してもらうといいでしょう。親御さんが聞いて理解できるように最後まで説明できていれば、お子さんもしっかり理解されていると思って問題ありません。
⑤ダイヤグラム
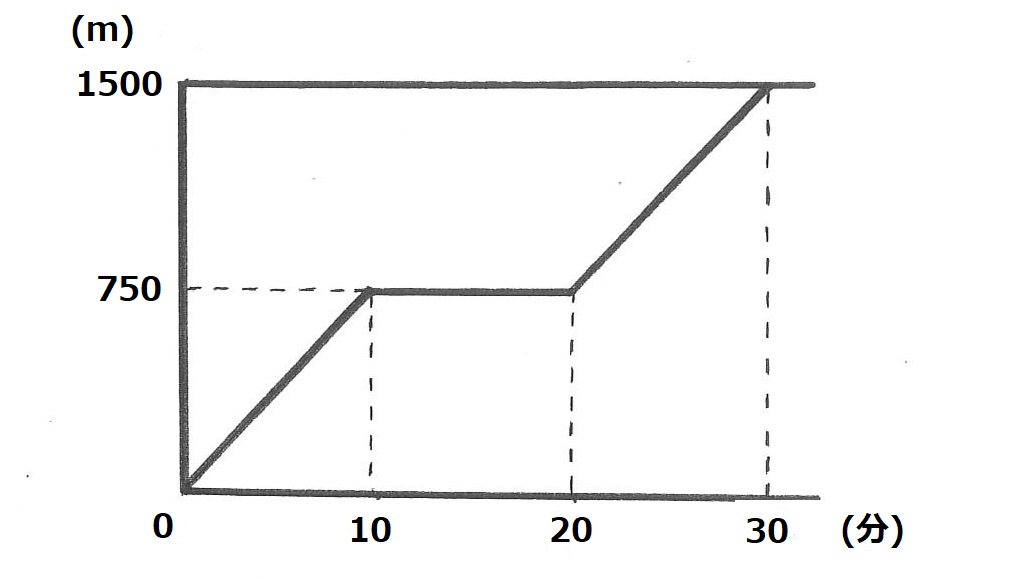
基本的なダイヤグラム
移動した時間と距離の関係をグラフに表したものを「ダイヤグラム」といいます。線分図と同じく人物などの動きを「視覚化」して条件を整理するためのもので、簡単なものであれば5年生から習います。
しかし、この「ダイヤグラム」を使う問題には「平面図形」のテクニックを利用して相似形をみつけて解いていく難易度の高い問題が存在します。身につけてしまえば、とても大きな武器になるのですが、線分図との使い分けや短時間での綺麗な作図など、使いこなすには練習が必要です。
塾によって扱いに大きく差がある解法でもありますが、筆者は早い時期にダイヤグラムを多用しなくてもいいのではないかと考えています。ダイヤグラムでなければ解けない問題は少なく、ほとんどの問題は線分図で解き切ることができます。
まずは線分図での解法をマスターし、その後に余裕が出てきてからダイヤグラムの平面図形的アプローチを学んでも遅くないと考えています。
学年・時期別に身につけておきたい内容
ここからは学年や時期別に、身につけておきたい内容を紹介します。
4年~5年前期で身につけたい内容
4年後期から5年は作図の練習時期です。問題文を読んで条件を線分図に整理できるように練習していきましょう。焦って発展的な問題にまで踏み込むよりも、基本問題をきちんと図を使って解くことが出来るようになることのほうが大切です。
また、単位の換算に慣れていく必要があります。「速さ」「距離」「時間」に関して、それぞれの単位を素早く変換できるように反復練習しましょう。小数ではなく分数で処理していくことも重要な点です。分数での計算に不安がないかどうかも、ご家庭でチェックできるポイントとなります。
5年後期で身につけたい内容
5年前期までで習得した作図のテクニックに比の概念をプラスして、よりスピーディーに解く技術をマスターしていきます。平行して旅人算以外の速さの問題の基本を学んでいくのもこの時期です。時計算、流水算、通過算などの旅人算以外の速さの基礎を学びます。
基本的な解き方、考え方は今まで習ってきた旅人算と同じ。基本がしっかり身についていればマスターできるはずです。
6年前期で身につけたい内容
これまでに学習した内容で解ける問題の幅を広げていきます。ダイヤグラムを習う時期でもありますが、前述した通り基本問題の理解だけでも十分です。
この時期までに旅人算が得意単元になっていれば相似形を利用したダイヤグラムの問題にチャレンジしていくのもいいと思います。
ただし、基本は線分図による解法であることをくれぐれも意識しておきたいですね。前期にしっかり基本の解き方を固めましょう。
6年夏期以降に身につけたい内容
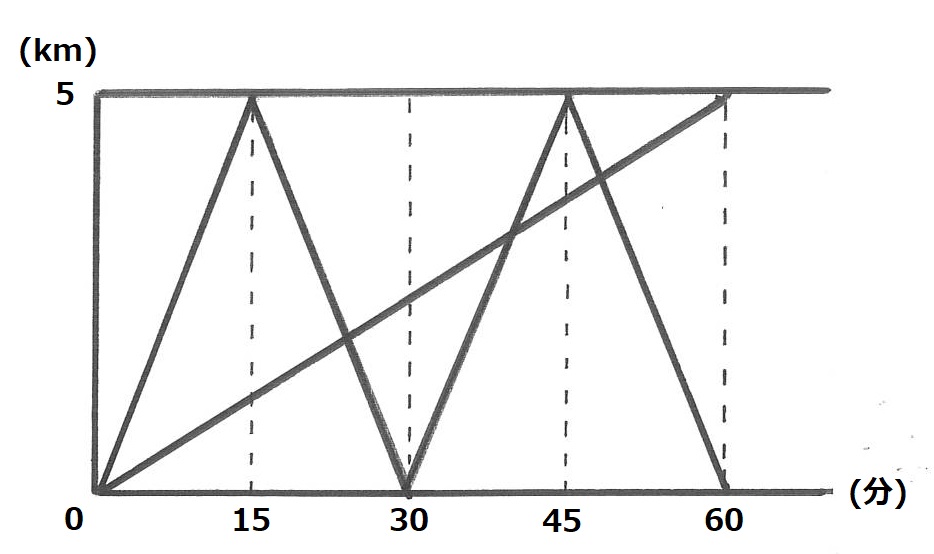
平面図形的アプローチを使って解くダイヤグラム
ここまで順調に基本的な力をつけられていれば、「ダイヤグラムを利用しての平面図形的アプローチ」「二人の間の距離の変化」といったワンランク上の難しい問題にチャレンジしていくことになります。
6年生後期はそれぞれの志望校の出題傾向に合わせて学習していく時期です。「グラフのついた問題が多い」「情報量が多くて複雑」「難易度は低いが速い処理が要求される」などといった各学校の特徴に合わせて弱点補強をしていきましょう。
まとめ
旅人算をマスターするのは簡単ではないかもしれません。そうだとは言え、何分考えても解き方がわからないような難問はほとんどないといっていいでしょう。
問題の多くは情報の整理の仕方と処理のスピードを問うものです。言い換えれば、きちんとしたプロセスを経て解く練習をしてきたかどうかの「努力量」が問われているということです。中学受験算数の単元のなかでも「努力しがいのある単元」と言えます。
一人でも多くの小学生が正しいアプローチで旅人算を得意単元にするために、この記事がお役に立てれば嬉しく思います。



コメント