中学受験の算数で、多くのお子さんが苦手意識を持っている「場合の数」。大手塾ではカリキュラムの中に何度も登場させて、少しずつ習得してもらうようにするのが一般的です。そのいっぽうで「塾のテキストで練習してもテストでなかなか得点できない」と悩んでいる受験生も多いように思います。この記事では、そんな“苦手分野No.1!”である「場合の数」の取り組み方のヒントを紹介します。
場合の数とは
「場合の数」とは「ある事柄について考えられる全ての場合を数え上げるときの総数」をいいます。
身近なところでは「ランチメニューの選び方」などが想像しやすいのではないでしょうか。前菜は3種類から選べて、パスタは5種類から選べて、ドリンクはコーヒーか紅茶の2種類付くランチでは、「前菜3通り」「パスタ5通り」「ドリンク2通り」なので「3×5×2=30」で合計30通りの選び方があります。これが「場合の数」です。
インターネットで「場合の数」と検索すると上位に表示されるのは高校数学の「場合の数」です。その内容やレベルは中学受験生が解くものと同じ。 つまり、中学受験生は高校生が解いている場合の数と同程度のものに取り組んでいるということになります。
この事実を知っておくことは重要です。小学生である中学受験生はそれぐらいハードルの高い問題に取り組んでいるのだという視点を持って、子供たちの取り組みをサポートしてあげたいものですね。
また、場合の数はケアレスミスによる失点が起きやすい単元でもあります。どんな単元でも「わかった」と「正解できる」は異なるものですが、場合の数は特にその差が大きい単元と言えるでしょう。言い換えれば、理解したうえで練習をしても点数につながりづらい単元ということになります。
「わかる」までも大変。そして「正解できる」ようになるまでにはケアレスミスをなくさなければならない。こんなハードルが待ち受けているのが、「場合の数」という単元なのです。
そんなやっかいな単元である場合の数では典型題のほか、かなり難易度の高い問題も出題されます。最難関校を志望するのであれば、かなりのレベルまで習得する必要があります。しかし、最難関校以外を受験するのであれば、「典型題はしっかり得点。難易度の高い問題は後回しにする」という作戦も時として正解になります。お子さんの理解度、志望校への出題頻度、出題されるものの難易度などを見極めながら取り組み方を変えていきましょう。
「場合の数」を学習する際の注意点
場合の数の学習を進めていくには、どのようなことに注意すればよいのでしょうか。
書き出しをマスター
3年生や4年生で習う場合の数の基本問題は、その全てを書き出して考えるものです。もれなく書き出して、その総数を数え上げる練習をします。ミスを防ぐ書き出し方、丁寧な書き出し、短時間での書き出しの工夫など、まずは「書き出す」という作業の仕方をマスターしたいものです。
樹形図などで書き出すものの中には計算で簡単に出せるものも少なくありませんが、まずは書き出しの仕方を習得するようにしましょう。樹形図がきちんと書けるようになったお子さんは、計算で解くときも「なぜその計算式になるのか」をきちんと理解できるようになります。
また、高難易度の問題では簡単に計算で出せるものは少なくなり、地道に書き出す作業が必須となります。場合の数で核となるのは、基本から応用まで「手を動かして書き出すこと」なのです。
典型題は反復が必要
書き出しができるようになると、典型題に関しては全てを書き出さなくても、短時間に計算で出せる方法を習います。塾のテキスト、学習されている問題集で「基本問題」とされている典型題は素早く答えを出せるようにしておきましょう。そのためには反復練習が欠かせません。数値の違った類題で何度も解く練習を積むことで正答率が上がっていきます。 典型題に関してはテストに出題されて必ず得点できるまで練習しましょう。
応用問題についての考え方
応用問題(各テストの正答率の低い問題)ができないからといって、すぐに場合の数の弱点補強に時間をとるのはおすすめできません。場合の数の応用問題は練習したからといって得点できるようになるとは限らない怖さがあるからです。まずは他の単元の習得に時間をつかうほうが合格に近づく可能性もあります。
ただし、サピックス偏差値55以上、四谷大塚偏差値62以上の学校を志望する場合には応用まで取り組む必要があります。お子さんの志望校の出題傾向や難易度をお通いの塾の先生に相談して取り組むべき範囲を指定してもらってもいいでしょう。
すべての受験生が習得すべき9つのタイプの典型題
ここからは、すべての受験生が必ず習得しておきたいベーシックな問題について紹介します。
並べる|樹形図を使って書き出す練習
【例題】
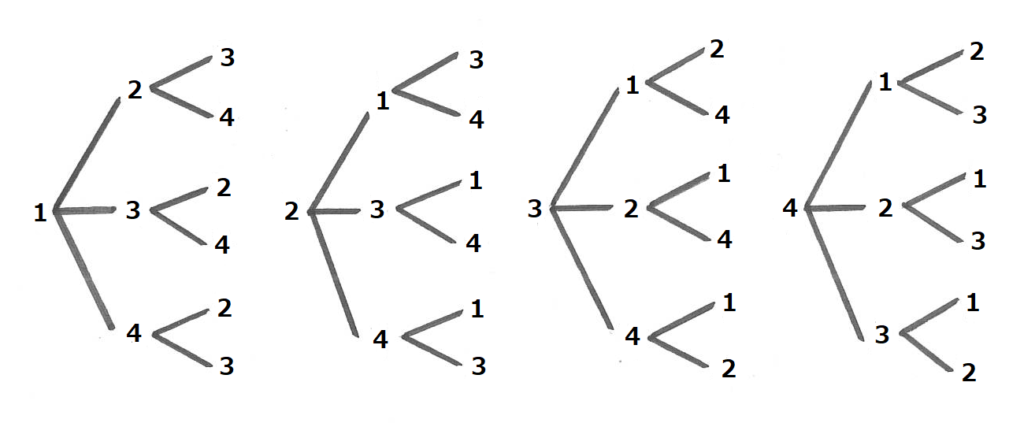
1,2,3,4の番号のかかれた4枚のカードから3枚を選んで3けたの整数を作るとき、全部で何個できますか。
場合の数の基本問題です。まずは樹形図を使って書き出す練習をして、そのあとに計算で求める方法を習得しましょう。「人を並べる」「色のついた球を並べる」などさまざまなバリエーションがあります。また、「0を含む、同じ数が複数枚ある」など条件によって難易度が上がっていきます。
選ぶ・選び方|「並べる」との区別をしっかりと
【例題】
6人の中から2人掃除当番を選びます。選び方は何通りありますか。
「6人の中から2人選んで並べる」場合としっかり区別します。「選ぶ」場合は順番が関係ないので、重複しているものを割り算で整理します。
例えば6人からAさんとBさんを選んで「並べる」場合は『AB』と並べる場合と『BA』と並べる場合を区別するので2通りと数えます。
一方6人からAさんとBさんを「選ぶ」場合は『AB』と選ぶのも『BA』と選ぶのも同一と考え、同じ選び方が2つ重複しているので、重複しているものを整理して2÷2=1通りとなります。
このように「並べる」のか「選ぶ」のかをしっかり問題文から読み取れる必要があるのです。「選ぶ」と「並べる」は場合の数の基礎となるのでしっかり学習したい内容です。
和分解|「もれなく」「重複なく」書き出す練習を
【例題】
サイコロを3回振って出た目の和が7になる場合は何通りありますか。
「和」を「分解」して考えます。基本的に書き出しによって解くことになるので反復練習が必要になります。「(1、1、5)(1、2、4)(1、3、3)……」というように「もれなく」「重複なく」書き出す必要があるので、塾の授業でお子さんが習ってくるやり方で練習してコツをつかみましょう。
また、「りんご7個とみかん5個の合計12個の果物を3人の子供に4個ずつ配ります。何通りの配り方がありますか。」といった問題も「和分解」の典型題です。正しい書き出し方を身に着けて、かつ反復して練習してもらいたい問題です。
カード並べ|ミスなく書き出すのがポイント
【例題】
0,1,4,5,6の番号の書かれた5枚のカードから3枚を選んで3けたの整数を作るとき、3の倍数は何通りできますか。
「並べる」だけの問題と違い、これは倍数の見分け方との複合問題で中学受験の典型題です。「もれなく書き出す」という作業にミスが出やすいため、塾で習って、解き方を理解してもなかなか得点できるようにならない問題でもあります。問題の解き方そのもの以外に、書き出すときのコツをしっかり習い、反復して練習をする必要がある問題です。
金額・お金|表を書いて、きれいに整理
【例題】
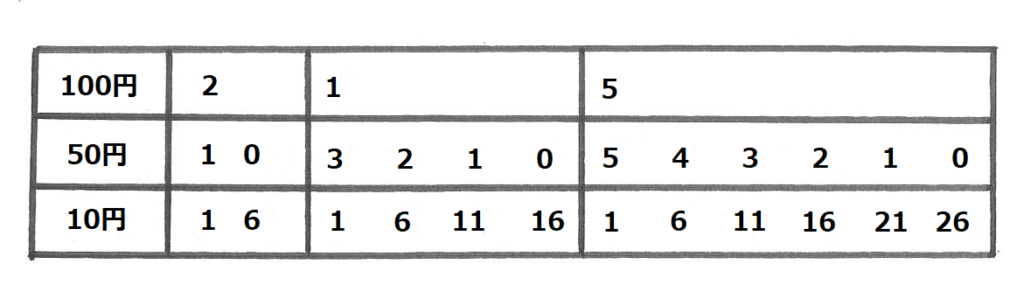
10円玉と50円玉と100円玉がたくさんあります。これらを使って260円ちょうどを支払う方法は何通りありますか。ただし使わない種類があってもよいものとします。
用意された硬貨で決められた金額を作る問題です。枚数制限が加わるとミスが増えます。表を書き、きれいに整理して書き出す練習をします。ここでも「もれなく」「条件に合うものだけ」書き出す作業にミスが出やすいものです。比較的余裕のある4、5年生の間にていねいに練習しておきたい問題です。
道順|本質的な理解が難問へのベースとなる
【例題】
図のような道をAからBまで遠回りせずに進むとき、行き方は全部で何通りありますか。
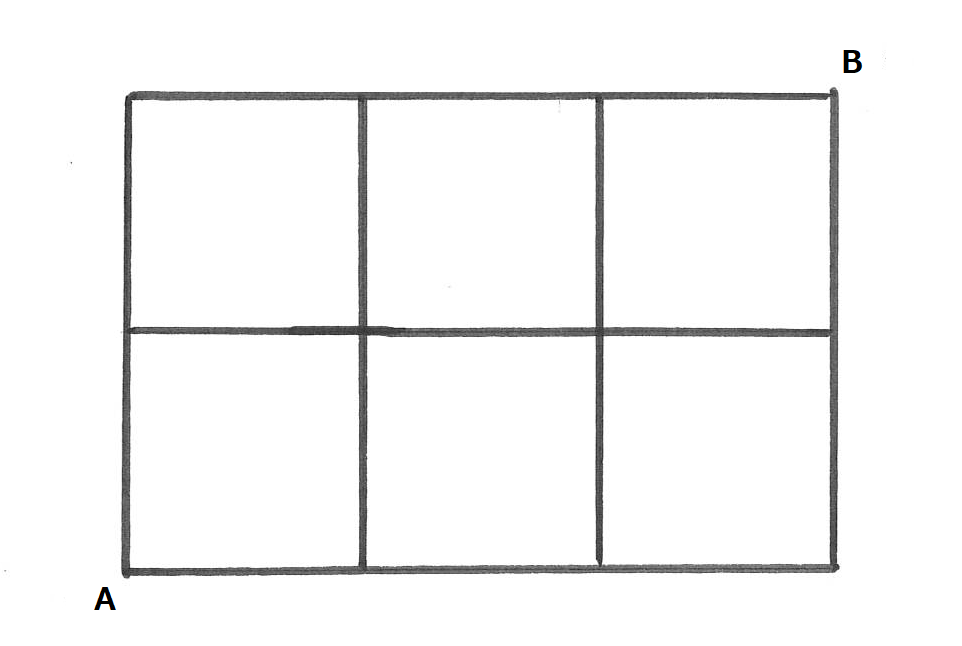
この問題は解き方を教われば、作業は複雑ではないのですぐに解けるようになります。しかし、なぜその計算式で答えが出るのかを本質的に理解できていないと、基本問題しか解けない状態に陥ってしまいます。塾のテキストでは少しずつ難易度を上げて類題を載せていますから、一つひとつ理解しながら進むようにしていきましょう。
ご家庭では「どうしてその式で答えが出るのかな?」と親御さんが質問してあげると良いと思います。 きちんと説明できることが理解できているサインです。
試合|「総当たり戦」と「トーナメント戦」をセットで習得
【例題】
5チームで野球の試合をします。総当たり戦で試合をする場合、何通りの組み合わせがありますか? また、トーナメント戦で優勝チームを決める場合、何試合必要ですか。
「総当たり戦」とは「全ての参加チームが全ての相手と対戦を行う方式」です。その組合せが何通りあるのかを問われます。
上記の例題の数値で説明すると、5チームから2チームを選び出して対戦する組合せの種類ということになるので、5人から2人を選ぶときの選び方と同様の解き方になります。
いっぽう「トーナメント戦」とは「勝者同士を戦わせて敗者を脱落させて最後まで勝ち残った者を優勝者とする方式」です。例題の数値で説明するなら5チームのうち4チームが敗者となれば優勝者が決まるので4試合という答えになります。解き方はいたってシンプルなのでお子さんが理解に苦しむというようなことはありません。
混乱してしまわないように「総当たり戦」と「トーナメント戦」をセットで理解しておくようにするとよいでしょう。出題の機会は多くないので解き方を忘れてしまうケースがよくあります。典型題として忘れないように何度か練習しておく必要があります。
ぬり分け|問題の難易度の差が大きい
【例題 】
図のような5つの部分を3色の絵具全てを使ってぬり分けます。何通りのぬり方がありますか。
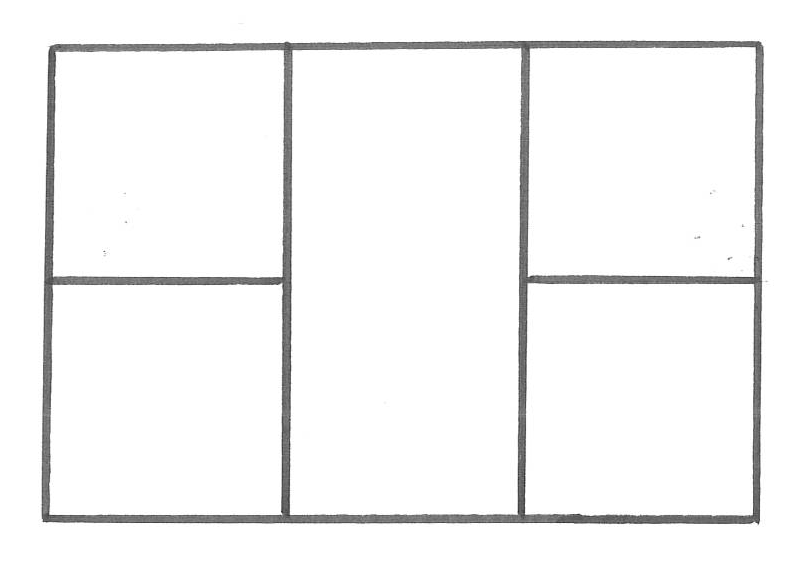
「ぬり分け」問題は、簡単な問題から非常に間違いやすい問題まで幅広いレベルのものが存在します。まず塾のテキストで扱う問題を習得して解き方の基本を身につけておきましょう。
過去問や模試などで難易度の高い問題が出ることがありますが、必ずしも得点しなければならない問題とは限りません。志望校の出題頻度が高くなければ基本問題だけで十分だと思います。
不定方程式|練習次第で必ず解けるようになる
【例題】
30円のお菓子Aと45円のお菓子Bをいくつか買って代金を300円にします。このとき、お菓子Aとお菓子Bの組み合わせは何通り考えられますか。
「つるかめ算」を利用して解くのだとも思ってしまいますが、合計の数がわかっていないので、解答が複数存在する「不定方程式」といわれる問題になります。高度な印象を持ってしまいがちな単元ですが、中学受験で扱うものは、もちろん算数の考え方だけで解き切ることのできるものです。
塾で習う解き方を類題で練習すれば必ず解けるようになります。難関校では他の特殊算と同様、不定方程式そのものが出題されるのではなく、大問を解いていく過程で必要となるツールといった位置づけになります。しっかりと解き方を習得しておきたい問題です。
まとめ
中学受験における「場合の数」は高校生が学習する内容と大差ないものが多くあります。そんな難しい単元に小学生である中学受験生が取り組んでいるのですから、習得を急かさずに応援してあげたいものですね。
また、難しすぎる問題に必要以上に取り組んでしまわないように、判断に迷った時には一緒に学習している先生に相談して、必要なものを見極めてあげるようにすることが大切です。




コメント